Operaciones Básicas De Conjuntos
Que es un conjunto
En matemáticas,
un conjunto es una
colección de objetos considerada como un objeto en sí. Los objetos de
la colección pueden ser cualquier cosa: personas, números, colores, letras, figuras,
etc. Cada uno de los objetos en la colección es un elemento o miembro del
conjunto.
Un conjunto
suele definirse mediante una propiedad que todos sus elementos poseen.
Un conjunto
queda definido únicamente por sus miembros y por nada más. En particular el
orden en el que se representen estos es irrelevante. Además, cada elemento
puede aparecer de manera idéntica una sola vez, esto es, no puede haber
elementos totalmente
idénticos repetidos.
Los conjuntos
pueden ser finitos o infinitos. El conjunto de
los número naturales es infinito, pero el conjunto de los planetas en
el Sistema Solar es finito (tiene
ocho elementos). Además, con los conjuntos pueden combinarse
mediante operaciones, de manera similar a las operaciones con
números.
 <------ CONJUNTO DE PERSONAS
<------ CONJUNTO DE PERSONAS
Que es una Unión
En la teoría de conjuntos,
la unión de dos (o
más) conjuntos es una operación que resulta en otro
conjunto cuyos elementos son los elementos de los conjuntos
iniciales. Por ejemplo, el conjunto de los números naturales es la
unión del conjunto de los números pares positivos P y el conjunto de los
número impares positivos I:
P = {2, 4, 6, ...}
I = {1, 3, 5, ...}
N = {1, 2, 3, 4, 5, 6, ...}
La unión
de conjuntos se denota por el símbolo ∪, de modo que por ejemplo, N = P ∪ I.
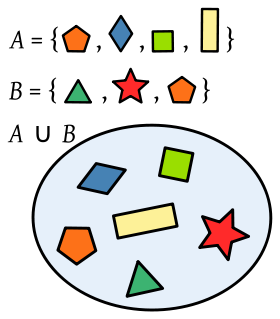 A:PERTENECE A UN CONJUNTO
A:PERTENECE A UN CONJUNTO
B: PERTENECE A OTRO CONJUNTO
EL CIRCULO DONDE APARECEN TODAS LAS FIGURAS JUNTAS DEL CONJUNTO A Y B SE LE LLAMA "UNIÓN"
Que es una Intersección
En teoría de conjuntos,
la intersección de dos (o
más) conjuntos es una operación que resulta en otro
conjunto que contiene los elementos comunes a los conjuntos de partida. Por
ejemplo, dado el conjunto de los números pares P y el conjunto de
los cuadrados C
de números
naturales, su intersección es el conjunto de los cuadrados pares D :
P = {2, 4, 6, 8, 10,...}
C = {1, 4, 9, 16, 25, ...}
D = {4, 16, 36, 64, ...}
La intersección
de conjuntos se denota por el símbolo ∩ por lo que D = P ∩ C.
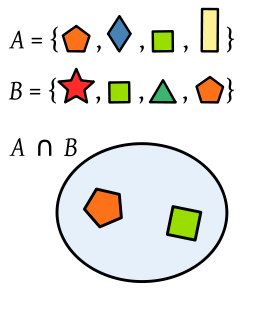 A: PERTENECE A UN CONJUNTO
A: PERTENECE A UN CONJUNTO
B: PERTENECE A OTRO CONJUNTO
EN EL CIRCULO SE MUESTRAN LAS FIGURAS QUE AL UNIR LOS CONJUNTOS A Y B COINCIDEN 2 FIGURAS, LAS CUALES SE REPITEN EN LOS 2 CONJUNTOS A ESO LE LLAMAMOS INTERSECCIÓN
A CONTINUACIÓN LES VOY A MOSTRAR UNA EXPLICACIÓN MAS BREVE
EN LA IMAGEN:
Nos muestra 2 círculos. Tomemos en cuenta solo el circulo azul que es el A.
A= (8, 6, 2, 4, 9) ESE CIRCULO Y LOS NÚMEROS QUE ESTÁN DENTRO DE EL, SON EL CONJUNTO.
Ahora tomemos solo en cuenta el circulo anaranjado que es el B.
B= (2, 7, 5, 3) ESE CIRCULO Y LOS NÚMEROS QUE ESTÁN DENTRO DE EL, TAMBIÉN SON UN CONJUNTO.
AHORA SI ESOS 2 CÍRCULOS A Y B LOS JUNTÁRAMOS, FORMARÍAMOS UNA UNIÓN LA CUAL ESTARÍA CONSTITUIDA POR:
A Y B= (8, 6, 2, 4, 9, 2, 7, 5, 3) JUNTANDO ESTOS 2 CIRCULOS ESTARÍAMOS UNIENDO TODOS LOS NÚMEROS
AHORA si se dan cuenta al hacer una unión de A Y B notamos que 1 numero se repite, el cual es el numero 2. Ese numero (2) es la intersección de la unión de dos conjuntos.
ALGO MAS FÁCIL SI NO LE ENTENDISTE:
TENEMOS A UNA JOVEN Y UN JOVEN, CADA UNO ES UN CONJUNTO, POR DECIRLO ASÍ, SI ELLOS 2 SE CASAN, TENEMOS AHÍ UNA UNIÓN, AHORA BIEN SI LOS 2 DECIDEN TENER UN BEBE, ESE SERIA LA INTERSECCIÓN, YA QUE VIENE DE ESA UNIÓN DE LOS JÓVENES QUE ELLOS DOS SOLOS ERAN UN CONJUNTO.

sabes ¿Cuáles son las operaciones básicas entre conjuntos?
ResponderEliminar2020 escape titanium - India's first ever, $350 - TITanium-arts
ResponderEliminarAt TITanium-arts 2014 ford fusion energi titanium India, we aim to show the first authentic Indian gaming experience titanium exhaust tubing in titanium trimmer as seen on tv India. titanium teeth A leading international designer and black titanium ring supplier,
j707d9fqkyf750 Rabbit Vibrators,dildos,dildos,male sex doll,glass dildos,black dildos,male sex toys,male sex dolls,sex toys f051m2qdkbm749
ResponderEliminar